HyperLogLog
- Kind of Probabilistic Data Structure
- Group of data structures that are extremely useful for big data and streaming applications
- These data structures use hash functions to randomize and compactly represent a set of items
- Collisions are ignored but errors can well-controlled under certain threshold
- Comparing with error-free approaches, these uses much less memory and have constant query time
- They supports union and intersection operations and therefore can be easily parallelized
- It’s a space-efficient algos. for accurate cardinality estimations
-
Redis’s implementation of HLL uses at most 12Kb of memory to estimate the cardinality of practically any set
- The Standard Error (SE) of the algorithm is defined as:
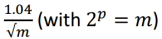
- where p is considered as a parameter of HLL specifying the desired accuracy.
- When one says “HyperLogLog 16-bit”, they mean that p = 16, making m = 216 = 65536
- Thus, by controlling the value of p, the accuracy of HLL’s cardinality estimation can be tuned
- Redis uses 14-bit HyperLogLog
- AdRoll uses 18-bit HyperLogLog
-
It is necessary to note that the higher the “p”, the more accurate the cardinality estimation
- By using a minimal amount of memory interms of KB, it can effectively represent hundreds of millions of distinct elements
HyperLogLog algo, thoroughly described in HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm
- Hashes each item in the set to be analyzed, obtaining an associated 32-bit binary number
- This value is then decomposed in two parts
- The first “b” bits of this value are used to determine which bucket of the *estimator this number falls in out of the **N = 2b</sub>** ones available*,
- And in the rest of the bits — we count the amount of leading zeros to estimate the probability of this number occurring.
- Every estimator bucket Mj,0 ≤ j < 2b, stores the maximum amount of leading zeros found for all the values associated with that bucket
- After all the items processed this way, the harmonic mean of the value 2Mj for all the buckets is calculated, this mean value will multiplied by a constant “Alpha” & amount of buckets “N”, the obtained result is raw HyperLogLog estimate, which can be expressed as
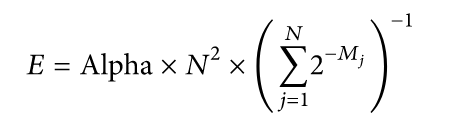

PseudoCode for HyperLogLog
- This algo applied to large data sets, the data to process is found in an input stream that is processed by chunks, which are groups of consecutive data taken from the stream, in the main loop of the algorithm
- The innermost loop takes care of the processing of each item in the current chunk.
- Each item is first hashed
- The resulting value is split into two pieces
- The 1st part of binary no. that represents the index of the estimator array For ex., when using 256 buckets, the index field corresponds to the 8 less significant bits of the hash, and the value 00010011 is the bucket number 35
- The rest of the bit stream is given to a function that counts the leading zeros and then the associated bucket is updated with this value if it is larger than the current value in the bucket. When the process finishes
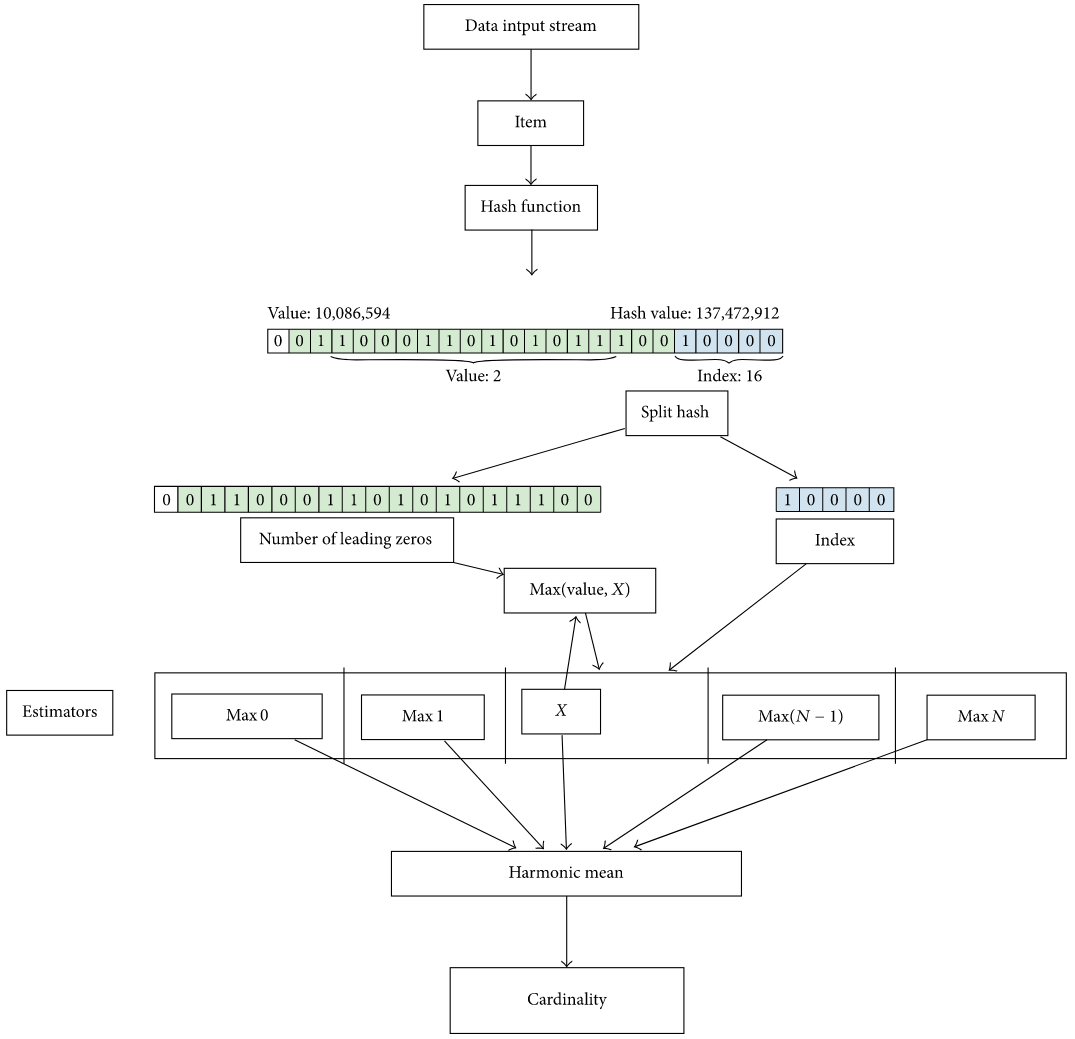 Sequential implementation of the HyperLogLog algorithm
Sequential implementation of the HyperLogLog algorithm
Programs
- OneMillionRecord
- A sample java program to display how to fetch data from .csv file which contains data set for quering purpose
- AddOneMillionInForHyperLogLog
- There are 3 .csv data set files which is used as i/o for HyperLogLog to find cardinality
- There 3 file all together may contains some duplicates data sets. So we also find the cardinality of 3 files using PFMerge function
| FileName (csv files) | Total DataSet Count | PFCount (cardinality) | TimeTaken (Secs) | Standard Error (SE) |
|---|---|---|---|---|
| urlFile1 | 1000000 | 998314 | 16.038 | 0.1686 |
| urlFile2 | 1000000 | 1003824 | 13.818 | 0.380943273 |
| urlFile3 | 1000001 | 998146 | 14.434 | 0.1854 |
cardinality of all 3 data sets using PFMerge function = 2583900
Note : Those 3 data sets may contains some common url sites
Conclusion
- This algorithm helps estimate the cardinality
-
Beside HyperLogLog, we have other Probabilistic Data Structure such as Count-Min Sketch for estimating frequencies, Bloom Filter for membership checking, etc. Thus, use the right data structure for the right purpose.
- Counting millions of distinct elements is a strength of HyperLogLog, But if we have few thousands of elements? In this case, maybe a simple Java HashSet or ArrayList can be enough